◄ OMMFem 2023

Gabriela encontró una enciclopedia de 2023 páginas, numeradas del 1 al 2023. Notó que las páginas cuyo número está formado únicamente por dígitos pares tienen una marca azul. También notó que cada tres páginas hay una marca roja, y que la primera marca roja está en la página 2. ¿Cuántas páginas de la enciclopedia están marcadas con ambos colores?

Matilda dibuja 12 cuadriláteros. El primer cuadrilátero que dibuja es un rectángulo de lados enteros y 7 veces más ancho que alto. Cada vez que termina de dibujar un cuadrilátero, une los puntos medios de cada pareja de lados consecutivos con segmentos de recta para así obtener el siguiente cuadrilátero. Se sabe que el último cuadrilátero que dibuja Matilda es el primero en tener área menor que 1. ¿Cuál es el área máxima posible del primer cuadrilátero?

Descargar Imagen

Un país llamado Máxico tiene dos islas, la isla Mayor y la isla Menor. La isla Mayor está compuesta por $k > 3$ estados, con exactamente $n > 3$ ciudades cada uno, de manera que tiene $kn$ ciudades en total. La isla Menor tiene sólo un estado, el cual tiene 31 ciudades. Dos aerolíneas de alto renombre, Aeropapantla y Aerocenzontle, ofrecen vuelos alrededor de Máxico. Aeropapantla ofrece vuelos directos desde cualquier ciudad hasta cualquier otra ciudad de Máxico. Aerocenzontle sólo ofrece vuelos directos desde cualquier ciudad de la isla Mayor hasta cualquier otra ciudad de la isla Mayor.\newline Cada aerolínea calcula qué porcentaje de sus propios vuelos directos conectan dos ciudades que se encuentran en el mismo estado. Así, se calcularon dos porcentajes en total, uno por cada aerolínea. Si sabemos que ambas aerolíneas obtuvieron el mismo porcentaje, ¿cuál es el menor número de ciudades que puede haber en la isla Mayor?

Se tiene una función $g$ tal que para todo entero $n$: \[g(n) = \begin{cases} 1 & \text{si } n\geq 1 \\ 0 & \text{si } n\leq 0 \end{cases}\] También se tiene una función $f$ que cumple lo siguiente para todos los enteros $n \geq 0$ y $m \geq 0$: \[f(0,m)= 0,\] \[f(n+1,m)=\left(1-g(m)+g(m)\cdot g(m-1-f(n,m))\right)\cdot\left(1+f(n,m)\right).\] Encuentra todas las posibles funciones f que cumplen estas condiciones. Es decir, encuentra todas las asignaciones $f (m, n)$ que cumplen las propiedades de arriba para todos los enteros $n \geq 0$ y $m \geq 0$.

Mía tiene 2 palitos verdes de $3cm$ cada uno, 2 palitos azules de $4cm$ cada uno y 2 palitos rojos de $5cm$ cada uno. Mía quiere formar un triángulo utilizando los 6 palitos como su perímetro, todos a la vez y sin encimarlos, doblarlos, o romperlos. ¿Cuántos triángulos no congruentes puede formar?

Alka encuentra escrito en un pizarrón un número $n$ que termina en 5. Realiza una secuencia de operaciones con el número en el pizarrón. En cada paso, decide realizar una de las dos operaciones siguientes:

1. Borrar el número escrito $m$ y escribir su cubo $m^3$.
2. Borrar el número escrito $m$ y escribir el producto $2023m$.

Alka realiza cada operación un número par de veces en algún orden y al menos una vez, y obtiene finalmente el número $r$. Si la cifra de las decenas de $r$ es un número impar, encuentra todos los valores posibles que la cifra de las decenas de $n^3$ pudo haber tenido.

Supongamos que $a$ y $b$ son números reales tales que $0 \lt a \lt b \lt 1$. Sean \[x = \frac{1}{\sqrt b}-\frac{1}{\sqrt{b+a}},\quad y = \frac{1}{b-a}-\frac{1}{b},\quad z = \frac{1}{\sqrt{b-a}}-\frac{1}{\sqrt b}.\] Muestra que $x$, $y$ y $z$ quedan siempre ordenados de menor a mayor de la misma manera, independientemente de la elección de $a$ y $b$. Encuentra dicho orden entre $x$, $y$ y $z$.

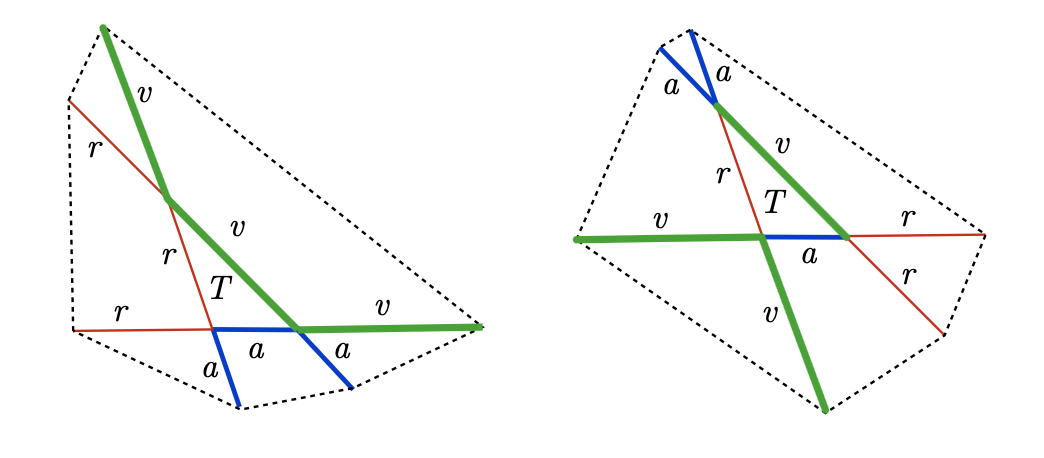
Se tienen 9 palitos de madera: 3 azules de longitud $a$ cada uno, 3 rojos de longitud $r$ cada uno y 3 verdes de longitud $v$ cada uno, tales que es posible formar un triángulo $T$ con palitos de colores todos distintos. Dana puede formar dos arreglos, comenzando con $T$ y utilizando los otros seis palitos para prolongar los lados de $T$, como se muestra en la figura. De esta manera, se pueden formar dos hexágonos cuyos vértices son los extremos de dichos seis palitos. Demuestra que ambos hexágonos tienen la misma área.

Descargar Imagen