OMMFem
OMMFem 2022 3
Se van a colorear todas las casillas de un tablero de $2022\times 2022$ de blanco o negro. En varias de estas casillas se van a colocar fichas, a lo más una por casilla. Decimos que dos fichas se atacan mutuamente, cuando se cumplen las siguientes dos condiciones:
¿Cuál es el máximo valor de $k$ tal que es posible colorear el tablero y colocar $k$ fichas sin que ningún par de ellas se ataquen mutuamente?
- Hay un camino de cuadritos que une las casillas en donde fueron colocadas las fichas. Este camino puede tener dirección horizontal, vertical, o diagonal.
- Todas las casillas en este camino, incluyendo las casillas donde están las fichas, son del mismo color.
¿Cuál es el máximo valor de $k$ tal que es posible colorear el tablero y colocar $k$ fichas sin que ningún par de ellas se ataquen mutuamente?
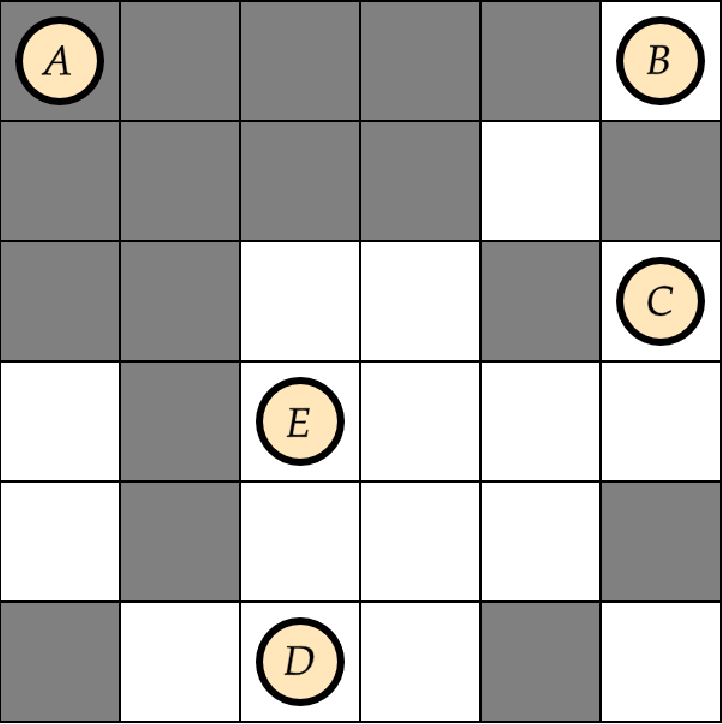
• Solución
• Regreso a OMMFem 2022