OMMFem 2022 ►

Sean $ABCD$ un cuadrilátero, $E$ el punto medio del lado $BC$, y $F$ el punto medio del lado $AD$ EL segmento $AC$ intersect a al segmento $BF$ en $M$ y al segmento $DE$ en $N$. Si a demás se sabe que el cuadrilátero $MENF$ es paralelogramo, demuestra que $ABCD$ también es un paralelogramo.

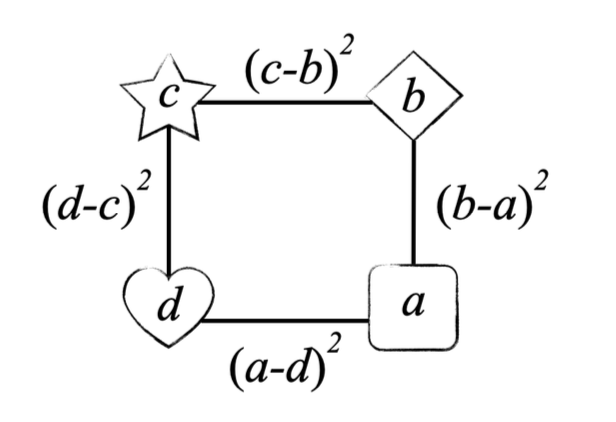
En el entrenamiento de un estado, la entrenadora les propone un juego. La entrenadora escribe en el pizarrón cuatro números reales en orden de menor a mayor: $a\lt b\lt c\lt d$. Cada olímpica dibuja en su cuaderno un cuadrado, y en los vértices coloca a $a$, $b$, $c$ y $d$. Una vez acomodados, sobre cada segmento escribe el cuadrado de la diferencia de los números en sus extremos. Después, suma los $4$ números obtenidos. Ganan las olímpicas que obtienen el menor resultado. ¿De qué maneras pueden ordenar los números para ganar? Da todas las soluciones.

Descargar Imagen

Se van a colorear todas las casillas de un tablero de $2022\times 2022$ de blanco o negro. En varias de estas casillas se van a colocar fichas, a lo más una por casilla. Decimos que dos fichas se atacan mutuamente, cuando se cumplen las siguientes dos condiciones:

• Hay un camino de cuadritos que une las casillas en donde fueron colocadas las fichas. Este camino puede tener dirección horizontal, vertical, o diagonal.
• Todas las casillas en este camino, incluyendo las casillas donde están las fichas, son del mismo color.

Por ejemplo, la figura muestra un ejemplo pequeño de una posible coloración de un tablero de $6\times 6$, con fichas $A$, $B$, $C$, $D$, y $E$ colocadas. Los pares de fichas que se atacan mutuamente son $(D,E)$, $(C,D)$, y $(B,E)$.
¿Cuál es el máximo valor de $k$ tal que es posible colorear el tablero y colocar $k$ fichas sin que ningún par de ellas se ataquen mutuamente?

Descargar Imagen

Sea $k$ un entero positivo y sea $m$ un entero impar. Prueba que existe un entero positivo $n$ tal que $n^n-m$ es divisible por $2^k$.

Una bióloga encontró un estanque con ranas. A la hora de clasificarlas por su masa notó lo siguiente: Las $50$ ranas más livianas representaban el $30\%$ de la masa total de todas las ranas del estanque, mientras que las $44$ ranas más pesadas representaban el $27\%$ de la masa total. Por las cosas del destino las ranas escaparon y la bióloga sólo cuenta con la anterior información. ¿Cuántas ranas había en el estanque?

Sean $a$ y $b$ enteros positivos tales que \[\frac{5a^4+a^2}{b^4+3b^2+4}\] es un número entero. Demuestra que $a$ no es un número primo.

Sea $ABCD$ un paralelogramo no rectángulo y sea $\Gamma$ la circunferencia que pasa por $A$, $B$, $D$. Sean $E$ y $F$ las intersecciones de $BC$ y $DC$ con $\Gamma$ respectivamente ($E\neq B$, $F\neq D$). Tenemos que los puntos $P$ y $Q$ son las intersecciones de $ED$ con $BA$ y de $FB$ con $DA$, respectivamente. Si las rectas $PQ$ y $CA$ se intersectan en $R$, muestra que: \[\frac{PR}{RQ}=\left(\frac{BC}{CD}\right)^2.\]

Sea $n$ un entero positivo. Considera un tablero en forma de triángulo equilátero, con lados de longitud $n$, dividido en triángulos equiláteros de lado $1$. Algunos de los $1+2+\dots+(n+1)$ vértices de los triangulitos equiláteros en los que se divide el tablero se han marcado. Se cumple que para todo entero $k\geq 1$, ningún trapecio con lados cuyas longitudes son $1$, $k$, $1$, $k+1$ y con vértices en el tablero tiene todos sus vértices marcados. Además, ningún triángulo equilátero de lado $1$ tiene sus tres vértices marcados. ¿Cuál es la mayor cantidad de vértices que se pudieron haber marcado?