OMM
OMM 2021 3
Sean $m,n\geq 2$ dos enteros. En una cuadrícula de $m\times n$, una hormiga empieza en el cuadrito inferior izquierdo y quiere caminar al camino superior derecho. Cada paso que da la hormiga debe ser a un cuadrito adyacente, y de acuerdo a las siguientes posibilidades: $\uparrow$, $\rightarrow$ y $\nearrow$. Sin embargo, un malvado mago ha dejado caer lava desde arriba de la cuadrícula y ha destruido algunos cuadritos, de forma tal que:
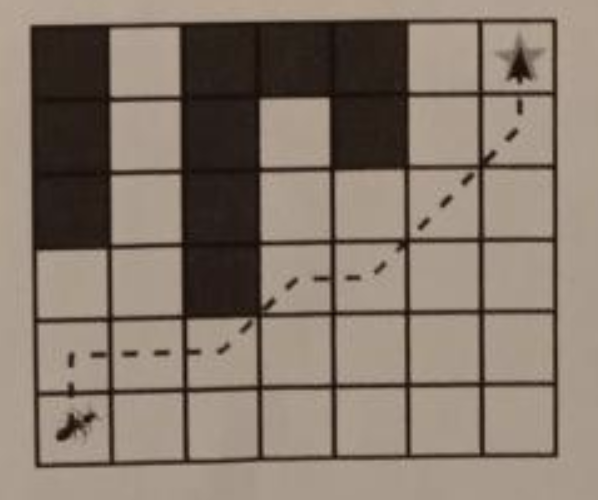
Nota: La longitud de un camino es el número de pasos que da la hormiga. Por ejemplo, se muestra un posible camino de longitud $8$ en la figura de $6\times 7$ siguiente, en la que los cuadritos destruidos están sombreados y la meta está indicada con una estrella.
- Si un cuadrito está destruido, entonces todos los cuadritos superiores a él también también están destruidos.
- El número de cuadritos destruidos es mayor o igual a $0$.
- Quedan suficientes cuadritos sin destruir para que la hormiga pueda llegar a la meta.
Nota: La longitud de un camino es el número de pasos que da la hormiga. Por ejemplo, se muestra un posible camino de longitud $8$ en la figura de $6\times 7$ siguiente, en la que los cuadritos destruidos están sombreados y la meta está indicada con una estrella.
• Solución
• Regreso a OMM 2021