◄ OMM 2021 ►
Presiona el título de cualquier problema para ver su página individual.
• Regresar a OMM• Regresar a la página de inicio
Problema 1
Los números reales positivos $a_1, a_2,a_3$ son tres términos consecutivos de una progresión aritmética, y análogamente, $b_1, b_2, b_3$ son números reales positivos distintos y términos consecutivos de una progresión aritmética. ¿Es posible utilizar tres segmentos de longitudes $a_1, a_2, a_3$ como bases, y otros tres segmentos de longitudes $b_1, b_2, b_3$ como alturas, para construir tres rectángulos de igual área?
Problema 2
Sea $ABC$ un triángulo tal que $\angle ACB>90^{\circ}$ y sea $D$ el punto de la recta $BC$ tal que $AD$ es perpendicular a $BC$. Considera $\Gamma$ la circunferencia de diámetro $BC$. Una recta que pasa por $D$ es tangente a la circunferencia $\Gamma$ en $P$, corta al lado $AC$ en $M$ (quedando $M$ entre $A$ y $C$) y corta al lado $AB$ en $N$. Demuestra que $M$ es punto medio de $DP$ si y solo si $N$ es punto medio de $AB$.
Problema 3
Sean $m,n\geq 2$ dos enteros. En una cuadrícula de $m\times n$, una hormiga empieza en el cuadrito inferior izquierdo y quiere caminar al camino superior derecho. Cada paso que da la hormiga debe ser a un cuadrito adyacente, y de acuerdo a las siguientes posibilidades: $\uparrow$, $\rightarrow$ y $\nearrow$. Sin embargo, un malvado mago ha dejado caer lava desde arriba de la cuadrícula y ha destruido algunos cuadritos, de forma tal que:
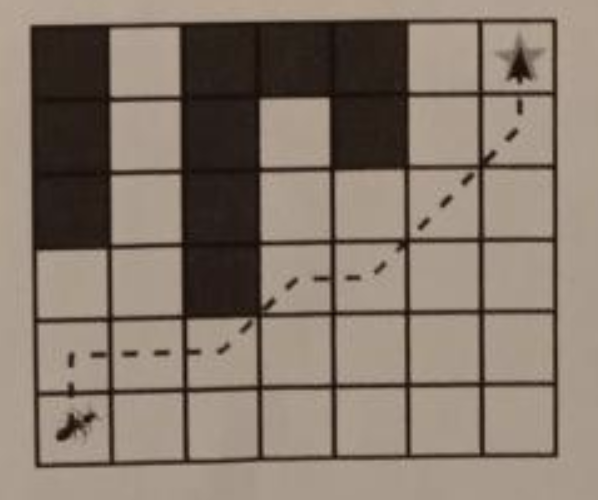
Nota: La longitud de un camino es el número de pasos que da la hormiga. Por ejemplo, se muestra un posible camino de longitud $8$ en la figura de $6\times 7$ siguiente, en la que los cuadritos destruidos están sombreados y la meta está indicada con una estrella.
- Si un cuadrito está destruido, entonces todos los cuadritos superiores a él también también están destruidos.
- El número de cuadritos destruidos es mayor o igual a $0$.
- Quedan suficientes cuadritos sin destruir para que la hormiga pueda llegar a la meta.
Nota: La longitud de un camino es el número de pasos que da la hormiga. Por ejemplo, se muestra un posible camino de longitud $8$ en la figura de $6\times 7$ siguiente, en la que los cuadritos destruidos están sombreados y la meta está indicada con una estrella.
Problema 4
Sea $ABC$ un triángulo acutángulo escálelo con $\angle BAC=60^{\circ}$ y ortocentro $H$. Sean $\omega_b$ la circunferencia que pasa por $H$ y es tangente a $AB$ en $B$, y $\omega_c$ la circunferencia que pasa por $H$ y es tangente a $AC$ en $C$.
- Prueba que $\omega_b$ y $\omega_c$ solamente tienen a $H$ como punto común.
- Prueba que la recta que pasa por $H$ y el circuncentro $O$ del triángulo $ABC$ es una tangente común a $\omega_b$ y $\omega_c$.
Problema 5
Para cada entero $n\lt 0$ con expansión decimal $\overline{a_1a_2\cdots a_{k-1}a_k}$, definimos a $s(n)$ como sigue:
Si $n$ es par, $s(n)=\overline{a_1a_2}+\overline{a_3a_4}\cdots+\overline{a_{k-1}a_k}$.
Si $n$ es impar, $s(n)=a_1+\overline{a_2a_3}\cdots+\overline{a_{k-1}a_k}$
Por ejemplo, si $n=123$, entonces $s(n)=1+23=24$ y si $n=2021$ entonces $s(n)=20+21=41$.
Decimos que $n$ es "digital" si $n$ es múltiplo de $s(n)$. Muestra que entre cualesquiera $198$ enteros positivos consecutivos, todos ellos menoress a $2000021$, hay uno de ellos que es digital.
Problema 6
Determina todos los conjuntos no vacíos $C_1, C_2, C_3, \cdots $ tales que cada uno de ellos tiene un número finito de elementos, y todos sus elementos son enteros positivos, con la siguiente propiedad: Para cualesquiera enteros positivos $n$ y $m$, el número de elementos del conjunto $C_n$ más el número de elementos del conjunto $C_m$ es igual a la suma de los elementos del conjunto $C_{m + n}$.
Nota: Al denotar por $\lvert C_k \lvert$ el número de elementos del conjunto $C_k$, y $S_k$ como la suma de los elementos del conjunto $C_k$, la condición del problema es que para cada $m,n$ enteros positivos se cumple
\[\lvert C_n \lvert + \lvert C_m \lvert = S_{n + m}.\]