OMM

OMM 2018 2

Para cada número entero positivo

m

, definimos

L_{m}

como la figura que se obtiene al superponer dos rectángulos de

1 \times 1

m \times 1

de manera que coincidan en el cuadrado de

1 \times 1

en sus extremos, como se muestra en la figura. Utilizando unas figuras

L_{m_{1}}, L_{m_{2}}, \dots, L_{m_{k}}

, cubrimos completamente un tablero

n \times n

, de forma que las aristas de la figura coincidan con líneas del tablero. Entre todas las coberturas posibles del tablero, encontrar el mínimo valor posible de

m_{1} + m_{2} + \dots + m_{k}

. Nota: Al cubrir el tablero, las figuras pueden estar giradas o reflejadas, y pueden solaparse o no estar completamente contenidas en el tablero.

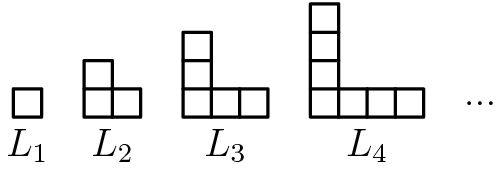
• Solución
• Regreso a OMM 2018