◄ OMM 2018 ►
Presiona el título de cualquier problema para ver su página individual.
• Regresar a OMM• Regresar a la página de inicio
Problema 1
Sean $A$ y $B$ dos puntos de una recta $\ell$, $M$ el punto medio de $AB$, y $X$ un punto del segmento $AB$ distinto de $M$. Sea $\Omega$ una semicircunferencia de diámetro $AB$. Consideremos un punto $P$ sobre $\Omega$ y sea $\Gamma$ la circunferencia que pasa por $P$ y $X$ que es tangente a $AB$. Sea $Q$ el segundo punto de intersección de $\Omega$ y $\Gamma$. La bisectriz del ángulo interno del $\angle PXQ$ interseca a $\Gamma$ en un punto $R$. Sea $Y$ un punto de $\ell$ tal que $RY$ es perpendicular a $\ell$. Muestra que $MX \gt XY$.
Problema 2
Para cada número entero positivo $m$, definimos $L_m$ como la figura que se obtiene al superponer dos rectángulos de $1 \times 1$ y $m\times 1$ de manera que coincidan en el cuadrado de $1 \times 1$ en sus extremos, como se muestra en la figura.
Utilizando unas figuras $L_{m_1}, L_{m_2}, \dots, L_{m_k}$, cubrimos completamente un tablero $n \times n$, de forma que las aristas de la figura coincidan con líneas del tablero. Entre todas las coberturas posibles del tablero, encontrar el mínimo valor posible de $m_1 + m_2 + \dots + m_k$.
Nota: Al cubrir el tablero, las figuras pueden estar giradas o reflejadas, y pueden solaparse o no estar completamente contenidas en el tablero.
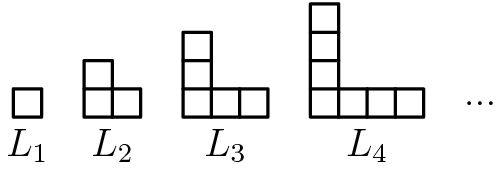
Problema 3
Una secuencia $a_2, a_3, \dots, a_n$ de enteros positivos se dice que es campechana, si para cada $i$ tal que $2 \leq i \leq n$ se cumple que exactamente $a_i$ términos de la secuencia son relativamente primos de $i$. Decimos que el tamaño de dicha sucesión es $n - 1$. Sea $m = p_1p_2 \dots p_k$, donde $p_1, p_2, \dots, p_k$ son primos distintos por parejas y $k \geq 2$. Muestra que existen al menos dos secuencias campechanas diferentes de tamaño $m$.
Problema 4
Sea $n\geq 2$ un número entero. Para cada pareja $k$ de enteros positivos $a_1, a_2, \ldots, a_k$ tal que $a_1+a_2+\cdots +a_k=n$, consideramos las sumas $S_i=1+2+\ldots +a_i$ para $1\leq i\leq k$. Determina, en términos de $n$, el máximo valor posible del producto $S_1S_2\cdots S_k$.
Problema 5
Sea $n\geq 5$ un número entero y consideremos un $n$-ágono regular. Inicialmente, Nacho se posiciona en uno de los vértices del $n$-ágono, en el que pone una bandera. Comienza a moverse en el sentido de las agujas del reloj. Primero se desplaza una posición y pone otra bandera, luego dos posiciones y pone otra bandera, etcétera, hasta que finalmente se desplaza $n-1$ posiciones y pone una bandera, de manera que pone $n$ banderas en total. ¿Para qué valores de $n$, Nacho habrá puesto una bandera en cada uno de los $n$ vértices?
Problema 6
Sea $ABC$ un triángulo acutángulo con circunferencia $\Omega$. Las bisectrices ángulos $B$ y $C$ intersectan a $\Omega$ en $M$ y $N$. Sea $I$ el punto de intersección de estas bisectrices. Sean $M'$ y $N'$ las respectivas reflexiones de $M$ y $N$ por $AC$ y $AB$. Muestra que el centro de la circunferencia que pasa por $I$, $M'$, $N'$ se encuentra en la altitud del triángulo $ABC$ desde $A$.