OMM

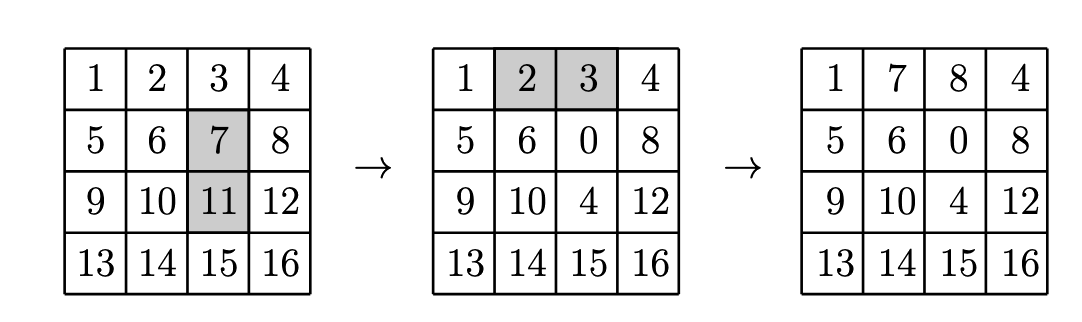
En una cuadrícula de $n \times n$ se escriben los números del $1$ al $n^2$ en orden, por renglones, de manera que en el primer renglón aparecen los números del $1$ al $n$, en el segundo los números de $n + 1$ a $2n$, y así sucesivamente. Una operación permitida en la cuadrícula consiste en escoger cualesquiera dos cuadraditos que compartan un lado y sumar (o restar) el mismo número entero a los dos números que aparecen en esos cuadraditos. Por ejemplo, abajo se muestran dos operaciones sucesivas permitidas en una cuadrícula de $4 \times 4$: primero restando $7$ a los cuadraditos sombreados y luego sumando $5$ a los sombreados. Determina para qué valores de $n$ es posible lograr que todos los cuadraditos tengan escrito el número $0$ después de repetir la operación tantas veces como sea necesario y, en los casos en que sea posible, determina el mínimo número de operaciones necesarias.

Descargar Imagen