◄ OMM 2015 ►

Sea $ABC$ un triángulo y sea $H$ su ortocentro. Sea $PQ$ un segmento que pasa por $H$ con $P$ en $AB$, $Q$ en $AC$ y tal que $\angle PHB = \angle CHQ$. Finalmente en el circuncírculo del triángulo $ABC$, considera $M$ el punto medio del arco $BC$ que no contiene a $A$. Muestra que $MP = MQ$.

Sea $n$ un entero positivo y $k$ un entero entre $1$ y $n$. Se tiene un tablero de $n \times n$ color blanco. Se hace el siguiente proceso. Se dibujan $k$ rectángulos con lados de longitud entera, con lados paralelos a los del tablero y tales que su esquina superior derecha coincide con la del tablero. Luego, estos $k$ rectángulos se rellenan de negro. Esto deja una figura blanca en el tablero. ¿Cuántas figuras blancas diferentes podemos obtener, que no se puedan obtener haciendo el proceso con menos de $k$ rectángulos? 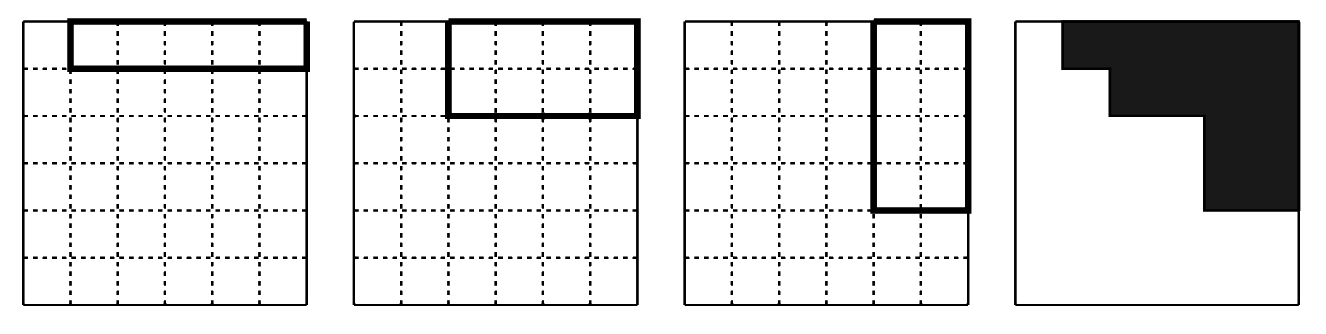Nota: A continuación se muestra un ejemplo para un tablero de $6 \times 6$. Se dibujan $3$ rectángulos, uno de $1 \times 5$, uno de $2 \times 4$ y uno de $4 \times 2$, para obtener la figura blanca indicada en el tablero de la derecha.

Descargar Imagen

Sea $\mathbb{N} = \{1, 2, 3, \dots \}$ el conjunto de los números enteros positivos. Sea $f : \mathbb{N} \to \mathbb{N}$ una función, la cual asigna a cada número entero positivo, un número entero positivo. Supón que $f$ satisface las siguientes dos condiciones: a) $f(1) = 1$. b) Para todos $a, b$ enteros positivos, se cumple que \[f (a + b + ab) = a + b + f (ab).\] Encuentra el valor de $f(2015)$.

Sea $n$ un entero positivo. María escribe en un pizarrón las $n^3$ ternas que se pueden formar tomando tres enteros, no necesariamente distintos, entre $1$ y $n$, incluyéndolos. Después, para cada una de las ternas, María determina el mayor (o los mayores, en caso de que haya más de uno) y borra los demás. Por ejemplo, en la terna $(1, 3, 4)$ borrará los números $1$ y $3$, mientras que en la terna $(1, 2, 2)$ borrará sólo el número $1$. Muestra que, al terminar este proceso, la cantidad de números que quedan escritos en el pizarrón no puede ser igual al cuadrado de un número entero.

Sea $I$ el incentro de un triángulo acutángulo $ABC$. La recta $AI$ corta por segunda vez al circuncírculo del triángulo $BIC$ en $E$. Sean $D$ el pie de la altura desde $A$ sobre $BC$ y $J$ la reflexión de $I$ con respecto a $BC$. Muestra que los puntos $D$, $J$ y $E$ son colineales.

Sea $n$ un entero positivo y sean $d_1, d_2, \dots , d_k$ todos sus divisores positivos ordenados de menor a mayor. Considera el número \[f (n) = (-1)^{d_1} d_1 + (-1)^{d_2} d_2 + \dots + (-1)^{d_k} d_k\] Por ejemplo, los divisores positivos de $10$ son $1$, $2$, $5$ y $10$, así que \[f (10) = (-1)^1 \cdot 1 + (-1)^2 \cdot 2 + (-1)^5 \cdot 5 + (-1)^{10} \cdot 10 = 6.\] Supón que $f (n)$ es una potencia de $2$. Muestra que si $m$ es un entero mayor que $1$, entonces $m^2$ no divide a $n$.