OMM

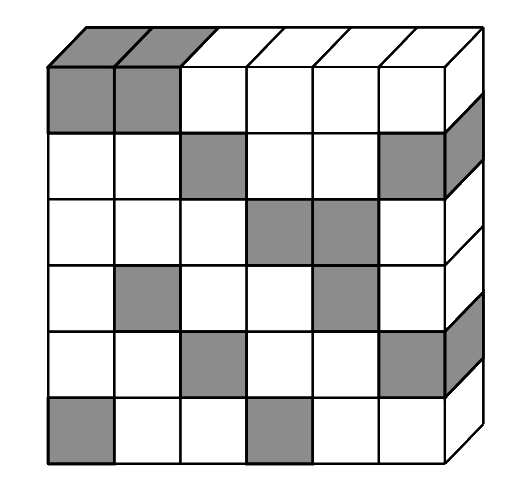
Un cubo de $n \times n \times n$ está construido con cubitos de $1 \times 1 \times 1$, algunos negros y otros blancos, de manera que en cada uno de los subprismas de $n\times 1\times 1$, de $1\times n\times 1$ y de $1\times 1\times n$ hay exactamente dos cubitos negros y entre ellos hay un número par (posiblemente $0$) de cubitos blancos intermedios. Por ejemplo, en la ilustración, se muestra una posible rebanada del cubo de $6 \times 6 \times 6$ (formada por $6$ subprismas de $1 \times 6 \times 1$). Muestra que es posible sustituir la mitad de los cubitos negros por cubitos blancos para que en cada subprisma de $n \times 1 \times 1$, de $1 \times n \times 1$ y de $1 \times 1 \times n$ haya exactamente un cubito negro.

Descargar Imagen