◄ OMM 2013 ►

Se escriben los números primos en orden, $p_1 = 2, p_2 = 3, p_3 = 5,\dots$ Encuentra todas las parejas de números enteros positivos $a$ y $b$ con $a - b \geq 2$, tales que $p_a - p_b$ divide al número entero $2(a - b)$.

Sea $ABCD$ un paralelogramo con ángulo obtuso en $A$. Sea $P$ un punto sobre el segmento $BD$ de manera que la circunferencia con centro en $P$ y que pasa por $A$, corte a la recta $AD$ en $A$ y $Y$, y corte a la recta $AB$ en $A$ y $X$. La recta $AP$ intersecta a $BC$ en $Q$ y a $CD$ en $R$, respectivamente. Muestra que $\angle XPY = \angle XQY + \angle XRY$.

¿Cuál es la mayor cantidad de elementos que puedes tomar del conjunto de números enteros $\{1, 2, \dots , 2013\}$, de tal manera que entre ellos no haya tres distintos, digamos $a$, $b$, $c$, tales que $a$ sea divisor o múltiplo de $b - c$?

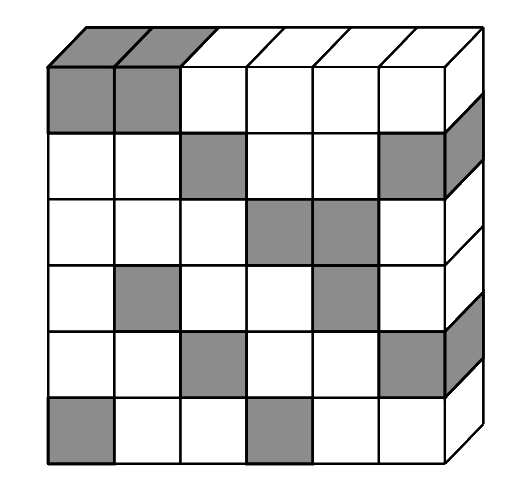
Un cubo de $n \times n \times n$ está construido con cubitos de $1 \times 1 \times 1$, algunos negros y otros blancos, de manera que en cada uno de los subprismas de $n\times 1\times 1$, de $1\times n\times 1$ y de $1\times 1\times n$ hay exactamente dos cubitos negros y entre ellos hay un número par (posiblemente $0$) de cubitos blancos intermedios. Por ejemplo, en la ilustración, se muestra una posible rebanada del cubo de $6 \times 6 \times 6$ (formada por $6$ subprismas de $1 \times 6 \times 1$). Muestra que es posible sustituir la mitad de los cubitos negros por cubitos blancos para que en cada subprisma de $n \times 1 \times 1$, de $1 \times n \times 1$ y de $1 \times 1 \times n$ haya exactamente un cubito negro.

Descargar Imagen

Una pareja de enteros es especial si es de la forma $(n, n - 1)$ o de la forma $(n - 1, n)$ con $n$ un entero positivo. Muestra que una pareja $(n, m)$ de enteros positivos que no es especial, se puede representar como suma de dos o más parejas especiales diferentes si y sólo si los enteros $n$ y $m$ satisfacen la desigualdad $n + m \geq (n - m)^2$.

Sea $A_1A_2 \dots A_8$ un octágono convexo, es decir, un octágono donde todos sus ángulos internos son menores que $180^{\circ}$. Además los lados del octágono tienen la misma longitud y cada par de lados opuestos son paralelos. Para cada $i = 1, \dots , 8$, definamos el punto $B_i$ como la intersección del segmento $A_iA_{i+4}$ con el segmento $A_{i-1}A_{i+1}$, donde $A_{j+8} = A_{j}$ y $B_{j+8} = B_j$ , para todo número entero $j$. Muestra que para algún número $i$, de entre los números $1, 2, 3$ y $4$, se cumple que \[\frac{A_iA_{i+4}}{B_iB_{i+4}} \leq \frac{3}{2}\]