◄ OMM 2006 ►

Sea $ab$ un número entero d dos dígitos. Un entero positivo $n$ es "pariente" de $ab$ si el dígito de las unidades de $n$ también es $b$, y los otros dígitos de $n$ son distintos de cero y suman $a$. Por ejemplo, los parientes de $31$ son $31$, $121$, $211$ y $1111$. Encuentra todos los números de dos dígitos que dividen a todos sus parientes.

Sea $ABC$ un triángulo rectángulo con ángulo recto en $A$, tal que $AB\lt AC$. Sean $M$ el punto medio de $BC$ y $D$ la intersección de $AC$ con la perpendicular a $BC$ que pasa por $M$. Sea $E$ la intersección de la paralela a $AC$ que pasa por $M$ con la perpendicular a $BD$ que pasa por $B$. Muestra que los triángulos $AEM$ y $MCA$ son semejantes si y solo si $\angle ABC=60^o$.

Sea $n$ un número entero mayor que $1$. ¿De cuántas formas se pueden acomodar todos los números $1,2,3,\dots 2n$ en las casillas de una cuadrícula de $2\times n$, uno en cada casilla, de manera que cualesquiera dos números consecutivos se encuentren en casillas que comparten un lado en la cuadrícula?

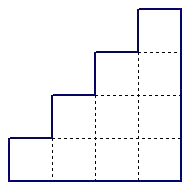
¿Para qué enteros positivos $n$ puede cubrirse una escalera como la de la figura (pero con $n$ escalones en vez de $4$) con $n$ cuadrados de lados enteros, no necesariamente del mismo tamaño, sin que estos cuadrados se encimen y sin que sobresalgan del borde de la figura?

Descargar Imagen

Sean $ABC$ un triángulo acutángulo y $AD$, $BE$ y $CF$ sus alturas. La circunferencia con diámetro $AD$ corta a los lados $AB$ y $AC$ en $M$ y $N$, respectivamente. Sean $P$ u $Q$ los puntos de intersección de $AD$ con $EF$ y $MN$, respectivamente. Muestra que $Q$ es el punto medio de $PD$.

Sea $n$ la suma de los dígitos de un entero positivo $A$. Decimos que $A$ es "surtido" si cada uno de los enteros $1,2,3,\dots ,n$ es la suma de algunos dígitos de $A$. Muestra que si $1,2,\dots ,8$ son sumas de algunos dígitos de un entero $A$, entonces $A$ es surtido. Si $1,2,\dots ,7$ son sumas de algunos dígitos de un entero $A$, ¿es $A$ necesariamente surtido? Nota: El número $117$ no es surtido porque no se puede sumar $3$ con algunos de sus dígitos, y $3<1+1+7$.