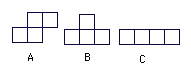◄ OMM 1994 ►

La secuencia $1, 2, 4, 5, 7, 9 ,10, 12, 14, 16, 17, ... $ se forma de la siguiente manera: Primero tomamos un número impar, luego dos números pares, luego tres números impares, luego cuatro números pares, y así sucesivamente. Encuentre el número de la secuencia que más se acerque a $1994$.

Los $12$ números en un reloj se reordenan. Muestra que existen tres números consecutivos con suma $21$ o más.

$ABCD$ es un paralelogramo. Sea $E$ un punto en la recta $AB$ tal que $BE = BC$ y $B$ está entre $A$ y $E$. La recta por $C$ perpendicular a $BD$ y la recta por $E$ perpendicular a $AB$ se intersectan en $F$. Muestra que $\angle DAF = \angle BAF$.

Un matemático caprichoso escribe un libro con páginas numeradas del $2$ al $400$. Las páginas las lee en el siguiente orden: El matemático toma la última página no leída ($400$), luego lee (en el orden normal) todas las páginas que no son relativamente primas a ella y que no se han leído antes. Repite este proceso hasta que haya leído todas las páginas. Así, el orden sería $2, 4, 5, ... , 400, 3, 7, 9, ... , 399, ...$. ¿Cuál es la última página que lee el matemático caprichoso?

$ABCD$ es un cuadrilátero convexo. Se toman los $12$ puntos que son los pies de las alturas de los triángulos $ABC, BCD, CDA, DAB$. Demuestra que al menos uno de estos puntos está sobre un lado de $ABCD$.

Muestra que es imposible embaldosar un tablero de $10\times 10$ con $25$ piezas del tipo $A$, ni con $25$ piezas del tipo $B$, ni con $25$ piezas del tipo $C$.

Descargar Imagen