◄ OMM 1989 ►
Presiona el título de cualquier problema para ver su página individual.
• Regresar a OMM• Regresar a la página de inicio
Problema 1
En un triángulo $ABC$ el área es $18$, la longitud $AB$ es $5$, y las medianas de $A$ y $B$ son ortogonales. Hallar las longitudes de los lados $BC,AC$.
Problema 2
Encontrar dos enteros positivos $a,b$ tales que $a | b^2, b^2 | a^3, a^3 | b^4, b^4 | a^5$, pero $a^5$ no divide a $b^6$.
Problema 3
Demostrar que no hay ningún número natural de $1989$ cifras que tenga al menos tres dígitos iguales a $5$ y que el producto de sus dígitos sea igual a su suma.
Problema 4
Encontrar el menor número natural posible $n = \overline{a_m ...a_2a_1a_0} $ (en sistema decimal) tal que el número $r = \overline{a_1a_0a_ma_{m-1} ...a_20} $ sea igual a $2n$.
Problema 5
Sean $C_1$ y $C_2$ dos circunferencias unitarias tangentes a una circunferencia $C$ de radio $2$. La circunferencia $C_3$ dentro de $C$ es tangente a las circunferencias $C,C_1,C_2$, y la circunferencia $C_4$ dentro de $C$ es tangente a $C,C_1,C_3$. Demostrar que los centros de $C_1,C_2,C_3$ y $C_4$ son vértices de un rectángulo.
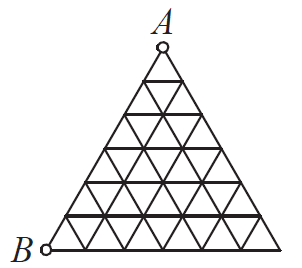
Problema 6
Determina el número de caminos desde $A$ a $B$ en la imagen que van sólo por las líneas de la cuadrícula, no pasan por ningún punto
punto dos veces, y nunca van hacia arriba?