◄ OMCC 2000 ►
Presiona el título de cualquier problema para ver su página individual.
• Regresar a OMCC• Regresar a la página de inicio
Problema 1
Encontrar todos los números naturales de tres dígitos $abc$ ($a\ne0$) tales que $a^2+b^2+c^2$ es divisor de $26$.
Problema 2
Determinar todos los enteros $n\ge1$ para los cuales es posible construir un rectángulo de lados $15$ y $n$ con piezas congruentes a las que se muestran a continuación.
Notas:
Las piezas no deben superponerse ni dejar huecos.
Los cuadritos de las piezas son de lado $1$.
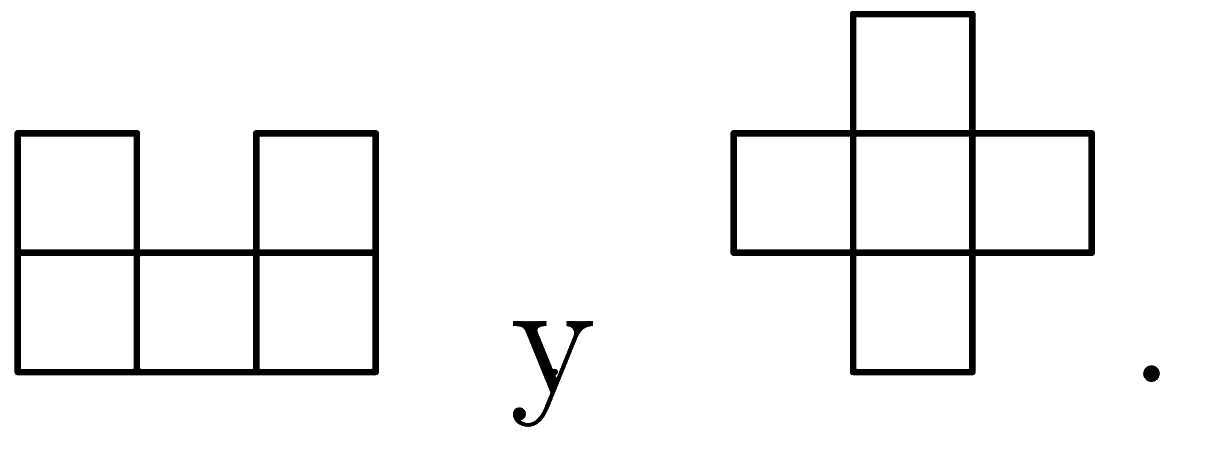
Problema 3
Sea $ABCDE$ un pentágono convexo. Sean $P,Q,R,S$ los baricentros de los triángulos $ABE,BCE,CDE$ y $DAE$, respectivamente. Demostrar que $PQRS$ es un paralelogramo y que su área es igual a $2/9$ el área del cuadrilátero $ABCD$.
Problema 4
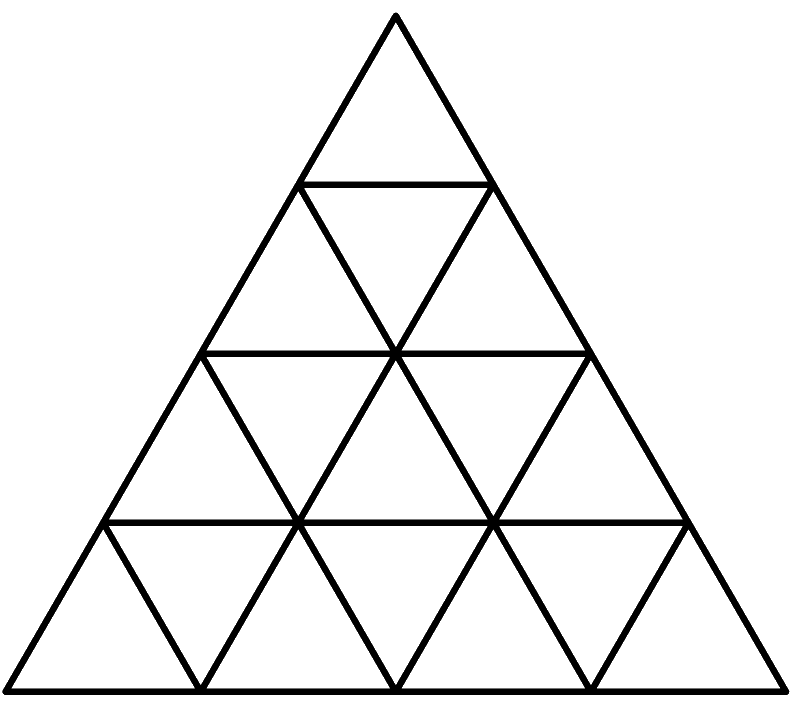
En la figura, escribir un entero positivo dentro de cada triangulito, de manera que el número escrito en cada triangulito que tenga al menos dos vecinos sea igual a la diferencia de los números escritos en algún par de vecinos. Dos triangulitos son vecinos si comparten un lado.
Problema 5
Sea $ABC$ un triángulo acutángulo, $C_1$ y $C_2$ dos circunferencias que tienen a los lados $AB$ y $CA$ como diámetros, respectivamente. $C_2$ corta al lado $AB$ en el punto $F$ y $C_1$ corta al lado $CA$ en el punto $E$. Además, $\overline{BE}$ corta a $C_2$ en $P$ y $\overline{CF}$ corta a $C_1$ en $Q$. Demostrar que $AP=AQ$.
Problema 6
Al escribir un entero $n\ge1$ como potencia de $2$ o como suma de potencias de $2$, donde cada potencia aparece a lo más dos veces en la suma, se tiene una \emph{representación buena} de $n$. Escriba las $5$ representaciones buenas de $10$ y determine que enteros positivos admiten un número par de representaciones buenas.