◄ IMO 2023

Determina todos los enteros compuestos $n \gt 1$ que satisfacen la siguiente propiedad: si $d_1,d_2,\dots,d_k$ son todos los divisores positivos de $n$ con $1 = d_1 \lt d_2 \lt \dots \lt d_k = n$, entonces $d_i$ divide a $d_{i+1} +d_{i+2}$ para cada $1\leq i\leq k-2$.

Sea $ABC$ un triángulo acutángulo con $AB \lt AC$. Sea $\Omega$ el circuncírculo de $ABC$. Sea $S$ el punto medio del arco $CB$ de $\Omega$ que contiene a $A$. La perpendicular por $A$ a $BC$ corta al segmento $BS$ en $D$ y a $\Omega$ de nuevo en $E \neq A$. La paralela a $BC$ por $D$ corta a la recta $BE$ en $L$. Sea $\omega$ el circuncírculo del triángulo $BDL$. Las circunferencias $\omega$ y $\Omega$ se cortan de nuevo en $P \neq B$. Demuestra que la recta tangente a $\omega$ en $P$ corta a la recta $BS$ en un punto de la bisectriz interior del ángulo $\angle BAC$.

Para cada entero $k \geq 2$, determina todas las sucesiones infinitas de enteros positivos $a_1,a_2,\dots$ para las cuales existe un polinomio $P$ de la forma $P(x) = x^k + c_{k-1}x^{k-1} + \dots + c_1x + c_0$, con $c_0,c_1,\dots,c_{k-1}$ enteros no negativos, tal que \[P(a_n)=a_{n+1}a_{n+2}\dots a_{n+k}\] para todo entero $n \geq 1$.

Sean $x_1, x_2, \dots , x_{2023}$ números reales positivos, todos distintos entre sí, tales que \[a_n = \sqrt{\left(x_1+x_2+\cdots+x_n\right)\left(\frac{1}{x_1}+\frac{1}{x_2}+\cdots+\frac{1}{x_n}\right)}\] es entero para todo $n = 1, 2, \dots , 2023$. Demuestra que $a_{2023} \geq 3034$.

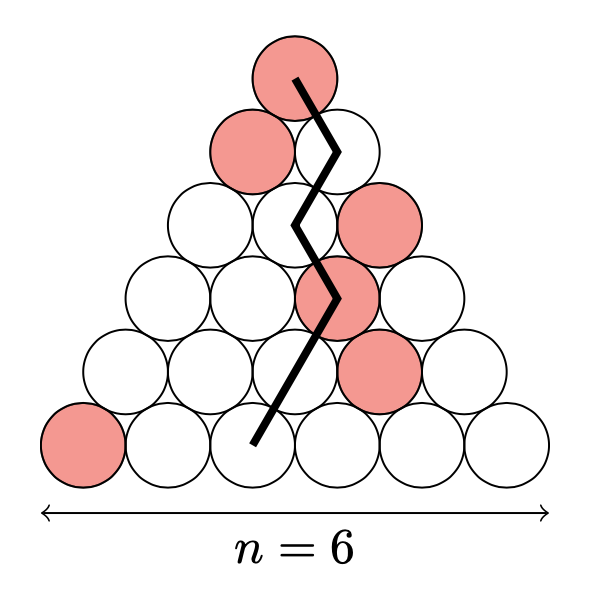
Sea $n$ un entero positivo. Un triángulo japonés consiste en $1 + 2 + \dots + n$ círculos iguales acomodados en forma de triángulo equilátero de modo que para cada $i = 1, 2, \dots , n$, la fila número $i$ contiene $i$ círculos, de los cuales exactamente uno de ellos se pinta de rojo. Un camino ninja en un triángulo japonés es una sucesión de $n$ círculos que comienza con el círculo de la fila superior y termina en la fila inferior, pasando sucesivamente de un círculo a uno de los dos círculos inmediatamente debajo de él. En el siguiente dibujo se muestra un ejemplo de un triángulo japonés con $n = 6$, junto con un camino ninja en ese triángulo que contiene dos círculos rojos.
En términos de $n$, determina el mayor $k$ tal que cada triángulo japonés tiene un camino ninja que contiene al menos $k$ círculos rojos.

Descargar Imagen

Sea $ABC$ un triángulo equilátero. Sean $A_1,B_1,C_1$ puntos interiores de $ABC$ tales que $BA_1 =A_1C$, $CB_1 =B_1A$, $AC_1 =C_1B$, y \[\angle BA_1C + \angle CB_1A + \angle AC_1B = 480^\circ.\] Las rectas $BC_1$ y $CB_1$ se cortan en $A_2$, las rectas $CA_1$ y $AC_1$ se cortan en $B_2$, y las rectas $AB_1$ y $BA_1$ se cortan en $C_2$. Demuestra que si el triángulo $A_1B_1C_1$ es escaleno, entonces los tres circuncírculos de los triángulos $AA_1A_2$, $BB_1B_2$ y $CC_1C_2$ pasan todos por dos puntos comunes.