◄ IMO 2004 ►
Presiona el título de cualquier problema para ver su página individual.
• Regresar a IMO• Regresar a la página de inicio
Problema 1
Sea $ABC$ un triángulo acutángulo con $AB\neq AC$. El círculo con diámetro $BC$ corta a los lados $AB$ y $AC$ en $M$ y $N$, respectivamente. Sea $O$ el punto medio del lado $BC$. Las bisectrices de los ángulos $\angle BAC$ y $\angle MON$ se intersecan en $R$. Muestra que los ciruncírculos de los triángulos $BMR$ y $CNR$ tienen un punto en común sobre el lado $BC$.
Problema 2
Encuentra todos los polinomios $f$ con coeficientes reales tales que para cualesquiera reales $a$, $b$, $c$, con $ab+bc+ca=0$, se cumple que
\[ f(a-b) + f(b-c) + f(c-a) = 2f(a+b+c). \]
Problema 3
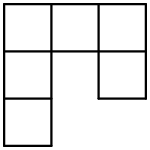
Definimos un "gancho" como una figura de 6 cuadritos unitarios como la que está en la imagen, o cualquier figura obtenida al aplicar rotaciones o reflexiones a la imagen. Encuentra todos los rectángulos de $m\times n$ que pueden ser cubiertos completamente sin hoyos ni sobrelaparse con ganchos.
Problema 4
Sea $n\geq 3$ un entero. Sean $t_1$, $t_2$, ..., $t_n$ reales positivos tales que \[n^2 + 1 \gt \left( t_1 + t_2 + \cdots + t_n \right) \left( \frac{1}{t_1} + \frac{1}{t_2} + \cdots + \frac{1}{t_n} \right).\]
Muestra que $t_i$, $t_j$, $t_k$ pueden ser las longitudes de los lados de un triángulo para toda $i$, $j$, $k$ tales que $1 \leq i \lt j \lt k \leq n$.
Problema 5
Sea $ABCD$ un cuadrilátero convexo tal que la diagonal $BD$ no bisecta al ángulo $ABC$ ni al ángulo $CDA$. El punto $P$ está dentro de $ABCD$ y cumple
\[\angle PBC=\angle DBA\quad\text{and}\quad \angle PDC=\angle BDA.\]
Muestra que $ABCD$ es cíclico si y sólo si $AP=CP$.
Problema 6
Decimos que un entero positivo es "alternativo" si cualesquiera dos dígitos consecutivos en su representación decimal tienen paridad distinta. Encuentra todos los enteros positivos $n$ tales que $n$ tiene un múltiplo alternativo.