◄ EGMO 2023

Se tienen $n\geq 3$ números reales positivos $a_1,a_2,\dots,a_n$. Para cada $1\leq i\leq n$ se define $b_i=\frac{a_{i-1}+a_{i+1}}{a_i}$, donde $a_0=a_n$ y $a_{n+1}=a_1$. Suponga que para cada $1\leq i\leq n$ cada $i\leq j\leq n$ se tiene que $a_i\leq a_j$ si y sólo si $b_i\leq b_j$.
Demuestre que $a_1=a_2=\dots =a_n$.

Sea $ABC$ un triángulo acutángulo y sea $D$ el punto sobre su circunferencia circunscrita tal que $AD$ sea un diámetro. Se escogen puntos $K$ y $L$ en los segmentos $AB$ y $AC$ respectivamente, tales que $DK$ y $DL$ son tangentes al círculo $AKL$. Demuestre que la recta $KL$ pasa por el ortocentro de $ABC$.

Sea $k$ un entero positivo. Alexa tiene un diccionario $\mathcal D$ que contiene algunas palabras de $k$ letras formadas sólo con las letras $A$ y $B$. En cada casilla de un tablero de tamaño $k\times k$, Alexa quiere escribir sólo la letra $A$ o la letra $B$, de tal manera que cada columna contenga una palabra de $\mathcal D$ cuando es leída de arriba a abajo y cada fila contenga una palabra de $\mathcal D$ cuando es leída de izquierda a derecha. ¿Cuál es el menor entero $m$ tal que si $\mathcal D$ contiene por lo menos $m$ palabras diferentes, entonces Alexa siempre puede llenar su tablero de esta manera, sin importar cuáles son las palabras que están en el diccionario $\mathcal D$?

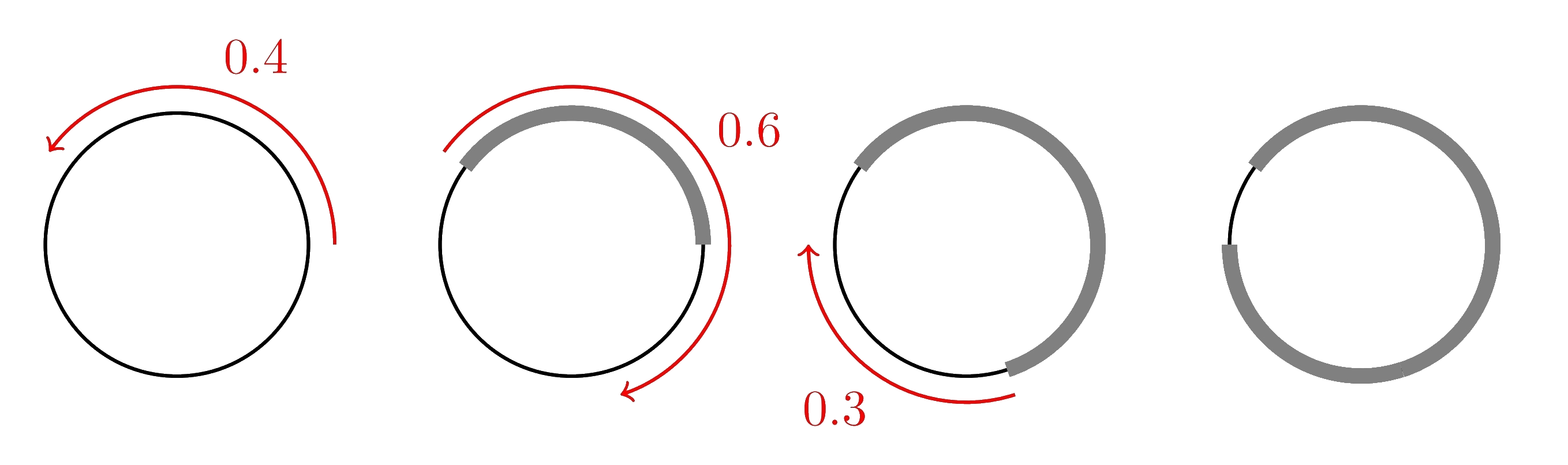
El caracolito Turbo está sobre un punto de una circunferencia de longitud 1. Sea $c_1,c_2,c_3,\dots$ una sucesión infinita de números reales positivos. Turbo se arrastra sucesivamente distancias $c_1,c_2,c_3,\dots$ sobre la circunferencia, eligiendo cada vez el sentido horario o antihorario. Por ejemplo, si la sucesión $c_1,c_2,c_3,\dots$ es $0.4,0.6,0.3\dots$, entonces Turbo podría haber elegido arrastrarse como en la figura. Determine la mayor constante $C\gt 0$ con la propiedad siguiente: para toda sucesión de números reales positivos $c_1,c_2,c_3,\dots$ tales que $c_1\lt C$ para todo $i$, Turbo puede asegurar (tras haber estudiado la sucesión) que hay un punto de la circunferencia por el que siempre puede evitar pasar.

Descargar Imagen

Sea $s\geq 2$ un entero positivo. Para cada entero positivo $k$ se define su torcimiento $k'$ como sigue: si $k$ se escribe como $as+b$, con $a,b$ enteros no negativos y con $b\lt s$, entonces $k'=bs+a$. Sea $n$ un entero positivo, considérese la sucesión infinita $d_1,d_2,\dots$ con $d_1 = n$ y $d_{i+1}$ el torcimiento de $d_i$ para cada $i$ entero positivo. Demuestre que esta sucesión contiene 1 si y sólo si el resto (o residuo) de la división de $n$ por $s^2-1$ es $1$ o $s$.

Sea $ABC$ un triángulo con circunferencia circunscrita $\Omega$. Se denota por $S_b$ y $S_c$ los puntos medios de los arcos $AC$ y $AB$ que no contienen el tercer vértice del triángulo, respectivamente. Sea $N_a$ el punto medio del arco $BAC$ (el arco $BC$ que contiene a $A$). Sea $I$ el incentro de $ABC$. Sea $\omega_b$ el círculo que es tangente a $AB$ y tangente internamente a $\Omega$ en $S_b$, y sea $\omega_c$ el círculo que es tangente a $AB$ y tangente internamente a $\Omega$ en $S_c$. Demuestre que la recta $IN_a$ y la recta que pasa por las intersecciones de $\omega_b$ y $\omega_c$, se intersectan sobre $\Omega$.